Signal Processing in Digital ICs
Introduction¶
In this case study, we show Pacti can work with a contract-based methodology to aid word-length optimization of digital signal processing integrated circuit design.
A digital signal processing system takes digital signals as inputs and generates the output signals by applying digital filters. The input signals are usually obtained through an analog-to-digital converter(ADC) from analog signals acquired from the environment by sensors. The impulse response of the digital filter is a set of coefficients that multiply with the input signals. The result is summed up to get the output signals.
Implementation of a digital filter in hardware is a time-consuming and error-prone process. To push the power, performance, and area to their limits, the floating-point operations are converted to fixed-point ones to reduce hardware costs and improve efficiency. However, the conversion incurs challenges, including the risk of overflow and lower accuracy. As a fixed-point number can represent smaller range than a floating-point one with the same number of bits, overflow might occur after the conversion. The fixed-point number with fewer bits tends to have lower accuracy as all bits in the fractional parts exceeding its fractional bits have to be discarded.
The following figure shows a multiplication operation using fixed-point numbers.
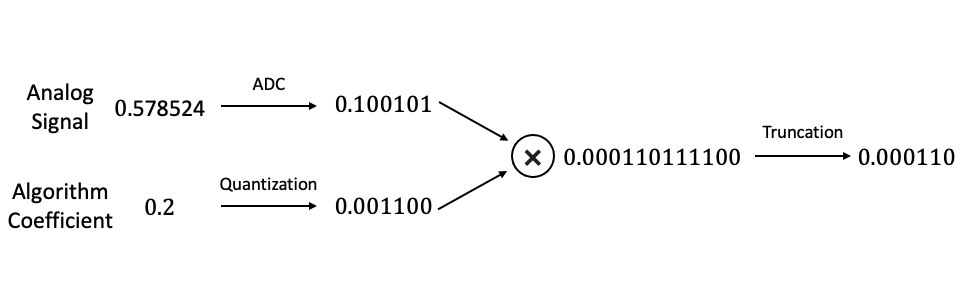
As a result, verifying and optimizing word length for fixed-point implementation is crucial for integrated circuit implementations. To prevent overflow and ensure the inaccuracy is acceptable, we need to bound the error of the system given the wordlength. In this case study, we apply contracts to compute the bounds of error of fixed-point arithmetic implementation.
Preliminaries¶
First, we introduce the fixed-point number.
Representation of Fixed-point Number¶
A word length of a fixed-point variable \(x\) can denoted as a tuple \((x_n, x_p)\), where \(x_n\) denotes the number of bits, and \(x_p\) is number of bits for the integer parts. For example, a fixed-point number with word length \((5,2)\) with bit value "11011" means the binary number \(11.011\), equivalent to \(3.375\) in decimal.
First, we import some data structure for holding the wordlength, and the APIs of Pacti.
"""DSP Case Study Code"""
import itertools
from tool import PortWordLength, float_to_bin, port_add, port_mult
from pacti.contracts import PolyhedralIoContract
# Definition of value_num method in PortWordLength class
# def value_num(self):
# return int(self.value, base=2) * 2 ** (- (self.n - self.p))
def show_wordlength() -> None:
"""Show the wordlength structure"""
port = PortWordLength(n=5, p=2, value="11011")
print(f'The word length (n = {port.n}, p = {port.p}) of the bits "{port.value}" is: ')
print(port.value_num())
show_wordlength()
The word length (n = 5, p = 2) of the bits "11011" is:
3.375
Error Sources in Fixed-point Arithmetic¶
The error of fixed-point arithmetic comes from the following sources: 1. Truncation Errors: A truncation error occurs when a fixed-point number is converted from a longer representation to a shorter one. As the number of bits is insufficient to represent the number perfectly, the least significant bits are truncated to match the word length. Truncation errors occur in fixed-point operations when the word length of the output variable is smaller than the ideal result. 2. Quantization Error: The quantization error occurs when an analog signal is converted into a digital one or when the coefficients are encoded into digital formats. As a fixed-point number cannot represent any real number with infinite precision, the signals and coefficients have to be quantized, and errors are introduced in the process. 3. Inaccurate Source: This error comes from the measurement in the analog signal because of noise and non-ideal effect on the sensor and could be seen as a random noise on the analog signal.
The following figure shows the three types of error in the example.
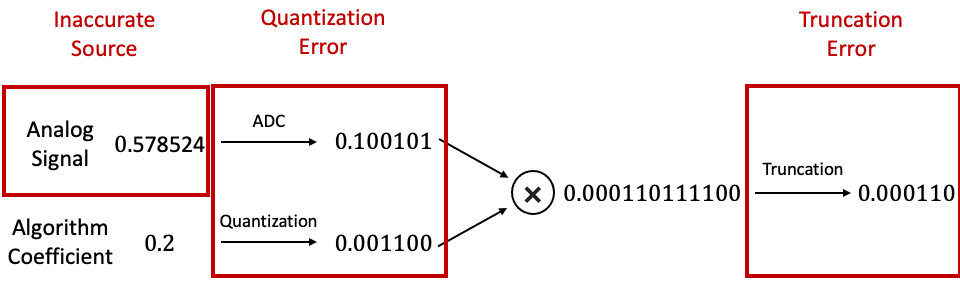
Given a input analog signal, the input signal and filter coefficients are first quantized into fixed-point numbers. Then the arithmetic operations, based on the algorithm or filter design, are performed on these fixed-point numbers. The results of the operations are truncated to fit into the fixed-point numbers of the output of the arithmetic operations.
During the process, differences between the fixed-point numbers representation and the ideal numbers result in errors. These errors propagate through the operations and thus affect the accuracy of the output signal.
Forming contract for capturing error of fixed-point number¶
Here we introduce how to form the contract for finding error bounds of the fixed-point number operation. First, we model the truncation errors and investigate how an operation result in the truncation errors. Then we consider the propagation of the error in different operations. We formulate the contract by combining the truncation errors and propagation of the error.
Modeling of Error from Operations¶
Each operation can be seen as a two-staged process. First, an ideal output with certain wordlength is generated without losing any accuracy, given the word lengths of all input ports. Then the ideal output is truncated to the actual output port. Therefore, the modeling of the ideal output wordlength and the truncation error is required to formulate the contract.
Operation Error Modeling¶
In the following, we detail how to model the truncation error. We divide the truncation error into two cases according to the number of bits for integer part.
Case 1: Identical Number of Bits in Integer Part¶
As the integer part has the same number of bits, overflow does not occur in this case. The least significant bits are truncated if the resulting word length is shorter. The maximal truncation error from the word length \((x_n, x_p)\) to the word length \((x_n', x_p)\) is \(2^{x_p}(2^{-x_n'}-2^{-x_n})\), when \(x_n > x_n'\). If \(x_n < x_n'\), there is no truncation, and thus the truncation error is exactly \(0\).
The following example shows how the error is bounded:
def truncation_error_same_position(pi: PortWordLength, po: PortWordLength) -> float:
"""
Truncation error for the case where input ports and output ports have the same number of integer bits.
Args:
pi: PortWordLength: input port word length
po: PortWordLength: input port word length
Returns:
The maximum truncation error if a number is truncated from wordlength pi to wordlength po
"""
assert pi.p == po.p
if pi.n > po.n:
return float(2**po.p * (2 ** (-po.n) - 2 ** (-pi.n)))
return 0
def truncate(pi: PortWordLength, po: PortWordLength) -> None:
"""
Truncate the value in pi into po.
Args:
pi: PortWordLength: input port word length
po: PortWordLength: input port word length
"""
# separate the bits into two parts, before binary point and after binary point
bits_str: str = str(pi.value)
bits_before_point = bits_str[: pi.p]
bits_after_point = bits_str[pi.p :]
# truncate or appending 0
if po.p >= pi.p:
bits_before_point = ("0" * (po.p - pi.p)) + bits_before_point
else:
bits_before_point = bits_before_point[pi.p - po.p :]
if po.n - po.p >= pi.n - pi.p:
bits_after_point = bits_after_point + "0" * (po.n - po.p - pi.n + pi.p)
else:
bits_after_point = bits_after_point[: (po.n - po.p)]
# combine the both parts
ret = bits_before_point + bits_after_point
po.value = ret
def example_truncation_error_same_position() -> None:
"""The example showing truncation error for same number of integer bits"""
p1 = PortWordLength(n=7, p=2, name="p1", value="1111111")
p2 = PortWordLength(n=5, p=2, name="p2")
print("Truncation Error: ")
print(truncation_error_same_position(p1, p2))
print("Example Value to produce the error")
truncate(p1, p2)
print(f"p1 = {p1.value_num()}, bits: {p1.value}")
print(f"p2 = {p2.value_num()}, bits: {p2.value}")
print("p1 - p2 = ", p1.value_num() - p2.value_num())
example_truncation_error_same_position()
Truncation Error:
0.09375
Example Value to produce the error
p1 = 3.96875, bits: 1111111
p2 = 3.875, bits: 11111
p1 - p2 = 0.09375
Then let's see what happens if the integer parts have different numbers of bits.
Case 2. Different Number of Bits in Integer Part¶
As the integer parts have different numbers of bits, overflow could occur if the resulting number cannot hold the original integer values. If an overflow occurs, the result deviates from the ideal value, and thus we expect no overflow occurs during the computation. This expectation will be applied as the assumption in subsequent parts when we formulate contracts.
Consider the case when converting a variable \(x\) with word length \((x_n, x_p)\) to the variable \(x'\) with word length \((x_n', x_p')\). We have to ensure that the value of \(x\) does not incur overflow in \(x'\). Therefore, it is reasonable to assume that we know that \(x\) is bounded by \(2^{x_p'}\) so that \(x'\) can represent the number without overflows.
Then, we can ignore the unnecessary most significant bits (\(x_p - x_p'\)), as they are always \(0\)s under the assumption. As a result, \((x_n, x_p)\) can be seen as \((x_n - x_p + x_p', x_p')\). The two numbers now have identical numbers of bits in their integer parts, and thus we can apply case 1 to get the truncation errors under the assumption.
The following example shows how the error can be calculated.
def truncation_error(pi: PortWordLength, po: PortWordLength) -> float:
"""
Truncation error for the case where input ports and output ports have different number of integer bits.
Args:
pi: PortWordLength: input port word length
po: PortWordLength: input port word length
Returns:
The maximum truncation error if a number is truncated from wordlength pi to wordlength po
"""
# remove uneccesary most significant bits
# Remider: The assumption must hold!!
pi_adjusted = PortWordLength(n=pi.n - pi.p + po.p, p=po.p)
# return the truncation error as in case 1
return truncation_error_same_position(pi=pi_adjusted, po=po)
def get_assumption_value(pi: PortWordLength, po: PortWordLength) -> float:
"""
Compute the assumption required for truncation to ensure no loss of integer values.
Args:
pi: PortWordLength: input port word length
po: PortWordLength: input port word length
Returns:
The maximum bound pi such that it won't loss integer bits after truncation
"""
if pi.p > po.p:
return float(2**po.p)
return float("inf") # no additional assumption needed
def check_assumption_value(pi: PortWordLength, po: PortWordLength) -> bool:
"""
Check if the value of the input port satisfy the assumption for truncation.
Args:
pi: PortWordLength: input port word length
po: PortWordLength: input port word length
Returns:
If the assumption to prevent integer bit loss is satisfied
"""
assumption_value = get_assumption_value(pi, po)
print(f"Assumption: {pi.name} < {assumption_value}")
if pi.value_num() >= assumption_value:
print("Assumption failed, truncation of MSB occurs")
return False
print(f"Assumption Satisfied ({pi.name} = {pi.value_num()} < {assumption_value})")
return True
def example_truncation_error() -> None:
"""Example showing the truncation error"""
p1 = PortWordLength(n=7, p=3, name="p1", value="0100111")
p2 = PortWordLength(n=5, p=2, name="p2")
assert check_assumption_value(pi=p1, po=p2)
print("Truncation Error: ")
print(truncation_error(p1, p2))
print("Example Value to produce the error")
truncate(p1, p2)
print(f"p1 = {p1.value_num()}, bits: {p1.value}")
print(f"p2 = {p2.value_num()}, bits: {p2.value}")
print("p1 - p2 = ", p1.value_num() - p2.value_num())
example_truncation_error()
Assumption: p1 < 4.0
Assumption Satisfied (p1 = 2.4375 < 4.0)
Truncation Error:
0.0625
Example Value to produce the error
p1 = 2.4375, bits: 0100111
p2 = 2.375, bits: 10011
p1 - p2 = 0.0625
Ideal Output Wordlength¶
Now we know how to get the truncation errors given the word length of two numbers, but what is the word length truncated in operations?
Each operation requires a minimum ideal output word length to fully hold the resulting value without losing any information. Assuming a binary operator, with inputs being \(x\) and \(y\) and output being \(z\), we represent the ideal output word length using \((z_n^*, z_p^*)\). The ideal output word length is then truncated to fit the output port.
Therefore, we need to know the ideal output word length for the operations. Let's first examine the addition and then the multiplication.
Addition¶
The following equations show the ideal output word length for addition.
\(z_n^* = \max(x_n, y_n - y_p + x_p) + \min(0, x_p - y_p) + 1\),
\(z_p^* = \max(x_p, y_p) + 1\).
The rationale behind the equations is to keep every bit from both inputs and include an additional bit for the carry.
def compute_required_word_length_add(in1: PortWordLength, in2: PortWordLength) -> PortWordLength:
"""
Compute the minimum word length to hold all values after addition operation on the inputs without lossing any information.
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
Returns:
The minimum word length to hold all values after addition operation on the inputs without lossing any information.
"""
new_n = max(in1.n, in2.n - in2.p + in1.p) - min(0, in1.p - in2.p) + 1
new_p = max(in1.p, in2.p) + 1
return PortWordLength(n=new_n, p=new_p)
def error_truncation_add(in1: PortWordLength, in2: PortWordLength, out: PortWordLength) -> float:
"""
Compute the maximum error of truncation caused by the addition operation.
The addition operation is perform for ports out = in1 + in2.
The value of in1 + in2 is truncated to fit in out
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
out: PortWordLength: output port word length
Returns:
The maximum error of truncation caused by the addition operation
"""
print(f"Input {in1.name}: (n={in1.n}, p={in1.p})")
print(f"Input {in2.name}: (n={in2.n}, p={in2.p})")
p_ideal = compute_required_word_length_add(in1=in1, in2=in2)
print(f"Ideal Output: (n={p_ideal.n}, p={p_ideal.p})")
print(f"Actual Output ({out.name}): (n={out.n}, p={out.p})")
assumption_value = get_assumption_value(pi=p_ideal, po=out)
print(f"Assumption: {in1.name} + {in2.name} < {assumption_value}")
return truncation_error(pi=p_ideal, po=out)
def example_truncation_error_add() -> None:
"""Example showing truncation error of addition operation"""
p1 = PortWordLength(n=7, p=3, name="p1", value="0100111")
p2 = PortWordLength(n=5, p=2, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
err = error_truncation_add(in1=p1, in2=p2, out=p3)
print(f"Error of the addition calculation: {err}")
example_truncation_error_add()
Input p1: (n=7, p=3)
Input p2: (n=5, p=2)
Ideal Output: (n=8, p=4)
Actual Output (p3): (n=5, p=3)
Assumption: p1 + p2 < 8.0
Error of the addition calculation: 0.1875
Multiplication¶
The following equations show the ideal output word length for multiplication.
\(z_n^* = x_n + y_n\),
\(z_p* = x_p, y_p\).
def compute_required_word_length_mult(in1: PortWordLength, in2: PortWordLength) -> PortWordLength:
"""
Compute the minimum word length to hold all values after multiplication operation on the inputs without lossing any information.
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
Returns:
The minimum word length to hold all values after multiplication operation on the inputs without lossing any information.
"""
new_n = in1.n + in2.n
new_p = in1.p + in2.p
return PortWordLength(n=new_n, p=new_p)
def error_truncation_mult(in1: PortWordLength, in2: PortWordLength, out: PortWordLength) -> float:
"""
Compute the maximum error of truncation caused by the multiplication operation.
The multiplication operation is perform for ports out = in1 * in2.
The value of in1 * in2 is truncated to fit in out
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
out: PortWordLength: output port word length
Returns:
The maximum error of truncation caused by the multiplication operation
"""
print(f"Input {in1.name}: (n={in1.n}, p={in1.p})")
print(f"Input {in2.name}: (n={in2.n}, p={in2.p})")
p_ideal = compute_required_word_length_mult(in1=in1, in2=in2)
print(f"Ideal Output: (n={p_ideal.n}, p={p_ideal.p})")
print(f"Actual Output ({out.name}): (n={out.n}, p={out.p})")
assumption_value = get_assumption_value(pi=p_ideal, po=out)
print(f"Assumption: {in1.name} * {in2.name} < {assumption_value}")
return truncation_error(pi=p_ideal, po=out)
def example_truncation_error_mult() -> None:
"""Example showing truncation error of multiplication operation"""
p1 = PortWordLength(n=7, p=3, name="p1", value="0100111")
p2 = PortWordLength(n=5, p=2, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
err = error_truncation_mult(in1=p1, in2=p2, out=p3)
print(f"Error of the multiplication calculation: {err}")
example_truncation_error_mult()
Input p1: (n=7, p=3)
Input p2: (n=5, p=2)
Ideal Output: (n=12, p=5)
Actual Output (p3): (n=5, p=3)
Assumption: p1 * p2 < 8.0
Error of the multiplication calculation: 0.2421875
Propagation of Error¶
Since fixed-point arithmetic incurs errors, the error could propagate through the previous operation to the final output. This error can be seen as independent of truncation error, as truncation errors are applied to the actual input numbers, which already contain the propagation errors. As a result, the error in the output variable \(z\), denoted as \(z_e\), can be represented as the sum of the propagation error and the truncation error in the stage:
\(z_e = z_{et} + z_{ep}\),
where \(z_{ep}\) is the propagation error from inputs, and \(z_{et}\) denotes the truncation error occurs in the operation.
Let's now see how the error is propagated in different operations.
General Operation¶
The propagation error is bounded by the maximum differences between the ideal value and the actual values. Therefore, the propagation errors can be modeled as follows:
\(z_{ep} = \max_{0<=x<=x_a, 0<=y<=y_a}(f(x, y)) - f(x-x_e, y-y_e))\),
where \(x_{a}\) and \(y_{a}\) is the upper bound of input variables \(x\) and \(y\), respectively.
According to this equation, we can derive the propagation error for addition and multiplication operations.
Propagation of Error in Addition¶
The error is exactly the sum of error from both inputs. \(z_{ep} = x_{e} + y_{e}\)
def error_propagation_add(in1: PortWordLength, in2: PortWordLength, out: PortWordLength) -> float:
"""
Compute the propagation error caused by addtion operation.
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
out: PortWordLength: output port word length
Returns:
The propagation error caused by addtion operation given the known error in the inputs.
"""
return float(in1.e + in2.e)
def example_propagation_error_add() -> None:
"""Example showing propagation error of addition operation"""
e1 = 0.5
e2 = 0.2
p1 = PortWordLength(n=7, p=3, e=e1, name="p1", value="0100111")
p2 = PortWordLength(n=5, p=2, e=e2, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
e_p = error_propagation_add(in1=p1, in2=p2, out=p3)
e_t = error_truncation_add(in1=p1, in2=p2, out=p3)
err = e_p + e_t
print(f"Propagation error: {e_p}")
print(f"Truncation error: {e_t}")
print(f"Error bound of the addition calculation: {err}")
example_propagation_error_add()
Input p1: (n=7, p=3)
Input p2: (n=5, p=2)
Ideal Output: (n=8, p=4)
Actual Output (p3): (n=5, p=3)
Assumption: p1 + p2 < 8.0
Propagation error: 0.7
Truncation error: 0.1875
Error bound of the addition calculation: 0.8875
Propagation of Error in Multiplication¶
The error is as follows:
\(z_{ep} = x_{a}*y_{e} + y_{a}*x_{e} - x_{e} * y_{e}\),
def error_propagation_mult(in1: PortWordLength, in2: PortWordLength, out: PortWordLength) -> float:
"""
Compute the propagation error caused by multiplication operation.
Args:
in1: PortWordLength: input port word length
in2: PortWordLength: input port word length
out: PortWordLength: output port word length
Returns:
The propagation error caused by multiplication operation given the known error in the inputs.
"""
return float(in1.a * in2.e + in2.a * in1.e + in1.e * in2.e)
def example_propagation_error_mult() -> None:
"""Example showing propagation error of multiplication operation"""
e1 = 0.5
e2 = 0.3
p1 = PortWordLength(n=7, p=3, e=e1, name="p1", value="0100111")
p2 = PortWordLength(n=5, p=2, e=e2, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
e_p = error_propagation_mult(in1=p1, in2=p2, out=p3)
e_t = error_truncation_mult(in1=p1, in2=p2, out=p3)
err = e_p + e_t
print(f"Propagation error: {e_p}")
print(f"Truncation error: {e_t}")
print(f"Error bound of the multiplication calculation: {err}")
example_propagation_error_mult()
Input p1: (n=7, p=3)
Input p2: (n=5, p=2)
Ideal Output: (n=12, p=5)
Actual Output (p3): (n=5, p=3)
Assumption: p1 * p2 < 8.0
Propagation error: 2.81875
Truncation error: 0.2421875
Error bound of the multiplication calculation: 3.0609375
Contract Formulation¶
We can formulate contracts for each operation by combining the modeling of error bounds from propagation and truncation. A contract is a pair of an assumption and a guarantee \(C = (A, G)\), where \(C\) represents the contract, \(A\) denotes its assumption, and \(G\) is the guarantee. In the following, we shall introduce the contract formulation for different operations.
Ports in Contract¶
Contracts specify system behaviors by describing the assignment of values in ports. For our case study, we see a variable \(x\) as a combination of two ports: the upper bound value port and the upper bound error port. The upper bound value port \(x_a\) tells the connected component the maximum value the variable can be, and the upper bound error port \(x_e\) passes the maximum error to the connected component.
Assumption¶
The assumption ensures no overflow occurs during the truncation, which has been introduced in the case where truncation involves two variables with different numbers of bits in the integer parts.
Guarantee¶
The guarantee of the contract includes two parts. The first part describes the upper bound value, and the second states the upper bound error.
The following functions show how we form contract for arbitrary length of input ports and output ports. The "_a" variables are used as the variable for the actual value going through the port.
def form_contract_add(
in_port1: PortWordLength, in_port2: PortWordLength, out_port: PortWordLength
) -> dict[str, object]:
"""
Create contract in dictionary form for an addition operation.
The contract includes information about the bound for its output value and the bound for its maximum error
Args:
in_port1: PortWordLength: input port word length
in_port2: PortWordLength: input port word length
out_port: PortWordLength: output port word length
Returns:
The contract in dictionary form for an addition operation.
"""
ret_contract: dict[str, object] = {}
# define input/output vars
ret_contract["input_vars"] = [
f"{in_port1.name}_a",
f"{in_port1.name}_e",
f"{in_port2.name}_a",
f"{in_port2.name}_e",
]
ret_contract["output_vars"] = [f"{out_port.name}_a", f"{out_port.name}_e"]
# get assumption
ideal_out_port = compute_required_word_length_add(in1=in_port1, in2=in_port2)
assumption_value = get_assumption_value(pi=ideal_out_port, po=out_port)
# write assumption in the contract
if assumption_value == float("inf"):
ret_contract["assumptions"] = []
else:
ret_contract["assumptions"] = [
{"coefficients": {f"{in_port1.name}_a": 1, f"{in_port2.name}_a": 1}, "constant": assumption_value}
]
# get guarantee
e_trunc = truncation_error(pi=ideal_out_port, po=out_port)
# write guarantee in the contract, note the propagation is encoded in the polyhedral constraints
ret_contract["guarantees"] = [
{
"coefficients": {f"{in_port1.name}_e": -1, f"{in_port2.name}_e": -1, f"{out_port.name}_e": 1},
"constant": e_trunc,
},
{"coefficients": {f"{out_port.name}_a": 1}, "constant": out_port.a},
# {"coefficients":{f"{out_port.name}_a": 1}, "constant":in_port1.a + in_port2.a},
{"coefficients": {f"{out_port.name}_a": 1, f"{in_port1.name}_a": -1, f"{in_port2.name}_a": -1}, "constant": 0},
]
return ret_contract
def form_contract_mult_const(
in_port: PortWordLength, in_port_const: PortWordLength, out_port: PortWordLength
) -> dict[str, object]:
"""
Create contract in dictionary form for a constant coefficient multiplication operation.
The contract includes information about the bound for its output value and the bound for its maximum error
Args:
in_port: PortWordLength: input port word length
in_port_const: PortWordLength: constant input port word length
out_port: PortWordLength: output port word length
Returns:
The contract in dictionary form for a constant coefficient multiplication operation.
"""
ret_contract: dict[str, object] = {}
# define input/output vars
ret_contract["input_vars"] = [f"{in_port.name}_a", f"{in_port.name}_e"]
ret_contract["output_vars"] = [f"{out_port.name}_a", f"{out_port.name}_e"]
# get assumption
ideal_out_port = compute_required_word_length_mult(in1=in_port, in2=in_port_const)
assumption_value = get_assumption_value(pi=ideal_out_port, po=out_port)
# write assumption in the contract
if assumption_value == float("inf"):
ret_contract["assumptions"] = []
else:
print(assumption_value)
ret_contract["assumptions"] = [
{"coefficients": {f"{in_port.name}_a": in_port_const.a}, "constant": assumption_value}
]
# get guarantee
print(ideal_out_port.to_string())
e_trunc = truncation_error(pi=ideal_out_port, po=out_port)
# write guarantee in the contract, note the propagation is encoded in the polyhedral constraints
ret_contract["guarantees"] = [
{
"coefficients": {
f"{in_port.name}_e": -in_port_const.a + in_port_const.e,
f"{in_port.name}_a": -in_port_const.e,
f"{out_port.name}_e": 1,
},
"constant": e_trunc,
},
{"coefficients": {f"{out_port.name}_a": 1}, "constant": out_port.a},
# {"coefficients":{f"{out_port.name}_a": 1}, "constant":in_port_const.a * in_port.a},
{"coefficients": {f"{out_port.name}_a": 1, f"{in_port.name}_a": -in_port_const.a}, "constant": 0},
]
return ret_contract
def example_contract_formulation() -> None:
"""Example of contract formulation"""
p1 = PortWordLength(n=7, p=3, name="p1")
p2 = PortWordLength(n=5, p=2, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
c1 = form_contract_add(in_port1=p1, in_port2=p2, out_port=p3)
print(c1)
contract1 = PolyhedralIoContract.from_dict(c1)
print(str(contract1))
e5 = 0.03
p4 = PortWordLength(n=7, p=3, name="p4")
p5 = PortWordLength(n=5, p=2, e=e5, value="11011", name="p5") # const
p6 = PortWordLength(n=5, p=3, name="p6")
c2 = form_contract_mult_const(in_port=p4, in_port_const=p5, out_port=p6)
contract2 = PolyhedralIoContract.from_dict(c2)
print(str(contract2))
example_contract_formulation()
{'input_vars': ['p1_a', 'p1_e', 'p2_a', 'p2_e'], 'output_vars': ['p3_a', 'p3_e'], 'assumptions': [{'coefficients': {'p1_a': 1, 'p2_a': 1}, 'constant': 8.0}], 'guarantees': [{'coefficients': {'p1_e': -1, 'p2_e': -1, 'p3_e': 1}, 'constant': 0.1875}, {'coefficients': {'p3_a': 1}, 'constant': 7.75}, {'coefficients': {'p3_a': 1, 'p1_a': -1, 'p2_a': -1}, 'constant': 0}]}
InVars: [p1_a, p1_e, p2_a, p2_e]
OutVars:[p3_a, p3_e]
A: [
p1_a + p2_a <= 8
]
G: [
-p1_e - p2_e + p3_e <= 0.1875
p3_a <= 7.75
-p1_a - p2_a + p3_a <= 0
]
8.0
Port: , (n, p) = (12, 5), e = 0, a = 31.9921875
InVars: [p4_a, p4_e]
OutVars:[p6_a, p6_e]
A: [
3.375 p4_a <= 8
]
G: [
-0.03 p4_a - 3.345 p4_e + p6_e <= 0.2422
p6_a <= 7.75
-3.375 p4_a + p6_a <= 0
]
Example 1¶
Consider the following simple system with two adders.
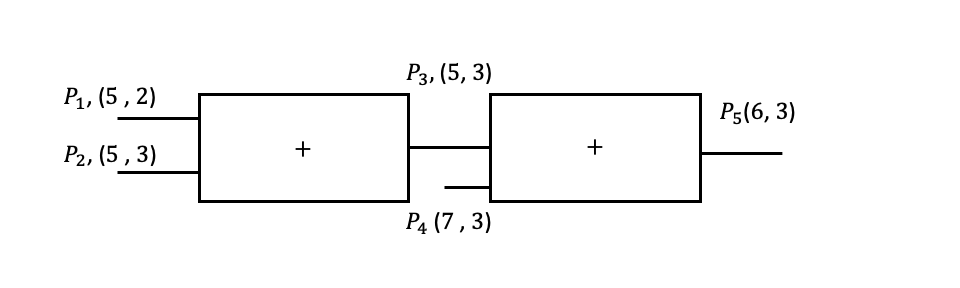
The word length is labeled beside the variable. We will show how Pacti can be applied to get the error bound for the word length.
First, we express each port using the PortWordLength class, and then form the contracts for the operations.
def create_example1() -> tuple:
"""
Generate the example contracts and ports for the example
Returns:
A tuple with 2 elements. The first one is the list of contract, and the other is the list of ports
"""
p1 = PortWordLength(n=5, p=2, name="p1")
p2 = PortWordLength(n=5, p=3, name="p2")
p3 = PortWordLength(n=5, p=3, name="p3")
c1 = form_contract_add(in_port1=p1, in_port2=p2, out_port=p3)
p4 = PortWordLength(n=7, p=3, name="p4")
p5 = PortWordLength(n=6, p=3, name="p5")
c2 = form_contract_add(in_port1=p3, in_port2=p4, out_port=p5)
contract1 = PolyhedralIoContract.from_dict(c1)
contract2 = PolyhedralIoContract.from_dict(c2)
contracts = [contract1, contract2]
ports = [p1, p2, p3, p4, p5]
return contracts, ports
We then use the composition to get the contract of the two adders.
def example_composition_two_adder() -> None:
"""Example of showing composition of two adder contracts"""
contracts, ports = create_example1()
contract1 = contracts[0]
contract2 = contracts[1]
print("Contract 1:\n" + str(contract1))
print("Contract 2:\n" + str(contract2))
contract_sys = contract1.compose(contract2)
print("Contract Sys:\n" + str(contract_sys))
example_composition_two_adder()
Contract 1:
InVars: [p1_a, p1_e, p2_a, p2_e]
OutVars:[p3_a, p3_e]
A: [
p1_a + p2_a <= 8
]
G: [
-p1_e - p2_e + p3_e <= 0.125
p3_a <= 7.75
-p1_a - p2_a + p3_a <= 0
]
Contract 2:
InVars: [p3_a, p3_e, p4_a, p4_e]
OutVars:[p5_a, p5_e]
A: [
p3_a + p4_a <= 8
]
G: [
-p3_e - p4_e + p5_e <= 0.0625
p5_a <= 7.875
-p3_a - p4_a + p5_a <= 0
]
Contract Sys:
InVars: [p1_a, p1_e, p2_a, p2_e, p4_a, p4_e]
OutVars:[p5_a, p5_e]
A: [
p4_a <= 0.25
p1_a + p2_a <= 8
]
G: [
-p1_e - p2_e - p4_e + p5_e <= 0.1875
-p4_a + p5_a <= 7.75
-p1_a - p2_a - p4_a + p5_a <= 0
p5_a <= 7.875
]
The composed contract shows the upper bound value and upper bound error of the output using the upper bound value and upper bound error of the inputs.
As we know the input word length, we can encode the input contracts with the upper bound value and upper bound error of the inputs. Let's see what will happen to the composition if we compose the contracts with the input contracts.
def form_contract_input(in_port: PortWordLength) -> dict[str, object]:
"""
Create contract in dictionary form for a input port to the system.
The contract includes information about the bound for its output value and the bound for its maximum error
Args:
in_port: PortWordLength: input port word length
Returns:
The contract in dictionary form for a input port to the system.
"""
ret_contract: dict[str, object] = {}
# define input/output vars
ret_contract["input_vars"] = []
ret_contract["output_vars"] = [f"{in_port.name}_a", f"{in_port.name}_e"]
# get assumption
ret_contract["assumptions"] = []
ret_contract["guarantees"] = [
{"coefficients": {f"{in_port.name}_a": 1}, "constant": in_port.a},
{"coefficients": {f"{in_port.name}_a": -1}, "constant": 0},
{"coefficients": {f"{in_port.name}_e": 1}, "constant": in_port.e},
{"coefficients": {f"{in_port.name}_e": -1}, "constant": -in_port.e},
]
return ret_contract
def composition_with_inputs(
contracts: list[PolyhedralIoContract], ports: list[PortWordLength]
) -> PolyhedralIoContract | None:
"""
Composition of the two adder system considering input infomation
Args:
contracts: list of PolyhedralIoContract for the adders
ports: list of port wordlengths for the ports
Returns:
The composition result if the composition is valid
"""
p1 = ports[0]
p2 = ports[1]
p4 = ports[3]
contract1 = contracts[0]
contract2 = contracts[1]
c_p1 = form_contract_input(in_port=p1)
c_p2 = form_contract_input(in_port=p2)
c_p4 = form_contract_input(in_port=p4)
contract_p1 = PolyhedralIoContract.from_dict(c_p1)
contract_p2 = PolyhedralIoContract.from_dict(c_p2)
contract_p4 = PolyhedralIoContract.from_dict(c_p4)
# compose the system
try:
contract_sys = contract1.compose(contract2)
except ValueError as e:
print("Composition Error")
print(e)
return None
try:
contract_sys = contract_p1.compose(contract_sys)
except ValueError as e:
print("Composition Error")
print(e)
return None
try:
contract_sys = contract_p2.compose(contract_sys)
except ValueError as e:
print("Composition Error")
print(e)
return None
try:
contract_sys = contract_p4.compose(contract_sys)
except ValueError as e:
print("Composition Error")
print(e)
return None
print("Contract Sys:\n" + str(contract_sys))
return contract_sys
def example_composition_without_input_bounds() -> None:
"""Example of composition without input bounds"""
contracts, ports = create_example1()
composition_with_inputs(contracts, ports)
example_composition_without_input_bounds()
Composition Error
Could not eliminate variables ['p2_a', 'p2_e', 'p5_a', 'p5_e']
by refining the assumptions
[
p2_a <= 4.125
]
using guarantees
[
p2_a <= 7.75
-p2_a <= 0
p2_e = 0
]
Then we consider the case where additional upper bound constraints are known for the inputs:
def example_composition_with_input_bounds() -> None:
"""Example of composition with correct input bounds"""
contracts, ports = create_example1()
p1 = ports[0]
p2 = ports[1]
p4 = ports[3]
p1.value = "10000"
p2.value = "01111"
p4.value = "0000001"
composition_with_inputs(contracts, ports)
example_composition_with_input_bounds()
Contract Sys:
InVars: []
OutVars:[p5_a, p5_e]
A: [
]
G: [
p5_a <= 5.812
p5_e <= 0.1875
]
In this case, we set the upper bound value of \(P_1\) to be \(4\), \(P_2\) to be \(3.75\), and \(P_4\) to be \(0.0625\). Under these input constraints, the operation is compatible with the inputs. And we obtain the composition results, which show the upper bound value and upper bound error of the output.
We can utilize Pacti to perform local optimization on word lengths. Given the system specification as a contract, word length optimization aims to reduce the word length while ensuring that the resulting implementation meets the system specification. Quotient is a contract operation that allows us to break down specifications to a certain subsystem. In this example, we try to reduce the word length of \(P_3\).

Since the word length of a variable affects the contract of operations that directly produce or use the variable, we can consider a subsystem consisting of those operations. For \(P_3\), the subsystem will be the composition of the two adders.
Assume our system specification is as follows:
which requires the upper bound error of the output \(P_5\) to be smaller than 0.1.We can invoke Pacti to compute the quotient to get the subsystem contract:
def get_desired_system_contract() -> PolyhedralIoContract:
"""
Generate contracts for the top-level specification
Returns:
The top-level specification contract
"""
ret_contract: dict[str, object] = {}
ret_contract["input_vars"] = []
ret_contract["output_vars"] = ["p5_a", "p5_e"]
ret_contract["assumptions"] = []
ret_contract["guarantees"] = [{"coefficients": {"p5_e": 1}, "constant": 0.1}]
return PolyhedralIoContract.from_dict(ret_contract)
def example_show_top_level_spec() -> None:
"""Example of showing the top level specification"""
contract_spec = get_desired_system_contract()
print("Top Level Specification:")
print(str(contract_spec))
example_show_top_level_spec()
Top Level Specification:
InVars: []
OutVars:[p5_a, p5_e]
A: [
]
G: [
p5_e <= 0.1
]
def quotient_example1() -> PolyhedralIoContract:
"""
Generate quotient based on the top-level specification and the system.
Returns:
The quotient result, the contract for the two adder operations
"""
contract_spec = get_desired_system_contract()
contracts, ports = create_example1()
p1 = ports[0]
p2 = ports[1]
p4 = ports[3]
p1.value = "10000"
p2.value = "01111"
p4.value = "0000001"
c_p1 = form_contract_input(in_port=p1)
c_p2 = form_contract_input(in_port=p2)
c_p4 = form_contract_input(in_port=p4)
contract_p1 = PolyhedralIoContract.from_dict(c_p1)
contract_p2 = PolyhedralIoContract.from_dict(c_p2)
contract_p4 = PolyhedralIoContract.from_dict(c_p4)
tmp_c1 = contract_spec.quotient(contract_p1)
tmp_c2 = tmp_c1.quotient(contract_p2)
return tmp_c2.quotient(contract_p4)
def example_quotient() -> None:
"""Example of showing using quotient to get contracts for the two adder operations"""
quotient_ret = quotient_example1()
print("Quotient of the Spec:")
print(str(quotient_ret))
example_quotient()
Quotient of the Spec:
InVars: [p1_a, p1_e, p2_a, p2_e, p4_a, p4_e]
OutVars:[p5_a, p5_e]
A: [
p1_a <= 2
-p1_a <= 0
p1_e = 0
p2_a <= 3.75
-p2_a <= 0
p2_e = 0
p4_a <= 0.0625
-p4_a <= 0
p4_e = 0
]
G: [
p5_e <= 0.1
]
The above contracts show the specification for the subsystem of two adders to meet such that the system contract can be implemented correctly. The refinement operation checks whether the selected word length meets the subsystem contract. This way of breaking down contracts into a subsystem allows us to reduce the problem size of the optimization. We can find the word length that satisfies the subsystem contracts for the two adders without considering the input constraints. As a result, we perform an exhaustive search to find the word length that meets the subsystem contract and, therefore, the system contract.
def create_example1_by_p3(p3_n: int, p3_p: int) -> tuple:
"""
Generate the example contracts and ports for the example, given different wordlength of p3
Args:
p3_n: the integer which defines the wordlength n for p3
p3_p: the integer which defines the wordlength p for p3
Returns:
A tuple with 2 elements. The first one is the list of contract, and the other is the list of ports
"""
p1 = PortWordLength(n=5, p=2, name="p1")
p2 = PortWordLength(n=5, p=3, name="p2")
p3 = PortWordLength(n=p3_n, p=p3_p, name="p3")
c1 = form_contract_add(in_port1=p1, in_port2=p2, out_port=p3)
p4 = PortWordLength(n=7, p=3, name="p4")
p5 = PortWordLength(n=6, p=3, name="p5")
c2 = form_contract_add(in_port1=p3, in_port2=p4, out_port=p5)
p1.value = "10000"
p2.value = "01111"
p4.value = "0000000"
contract1 = PolyhedralIoContract.from_dict(c1)
contract2 = PolyhedralIoContract.from_dict(c2)
# print("Contract 1:\n" + str(contract1))
# print("Contract 2:\n" + str(contract2))
contracts = [contract1, contract2]
ports = [p1, p2, p3, p4, p5]
return contracts, ports
def exhaustive_search() -> int:
"""
Perform exhaustive search on finding the minimum wordlength that satisfy the top-level specification
Returns:
The word length n for p3
"""
quotient_ret = quotient_example1()
for n in range(5, 10):
# print(n)
p = 3 # keep the same number of bits (2) before binary point
contracts, ports = create_example1_by_p3(p3_n=n, p3_p=p)
contract1 = contracts[0]
contract2 = contracts[1]
try:
contract_sys = contract1.compose(contract2)
# contract_sys = compose_all(contract1, contract2, p1, p2, p3, p4, p5)
# print(str(contract_sys))
except ValueError:
continue
if contract_sys.refines(quotient_ret):
return n
return -1
def example_word_length_optimization() -> None:
"""Example of showing word length optimization on p3 for the case study"""
n = exhaustive_search()
print(f"Wordlength for P3 to satisfy the spec is n = {n}")
example_word_length_optimization()
Wordlength for P3 to satisfy the spec is n = 6
And we successfully find the word length of 6 that meets the system specification.
Example 2: Filter Design¶
Now we apply the contract to a simple filter that computes the moving average of the input signal, as shown in the figure below,
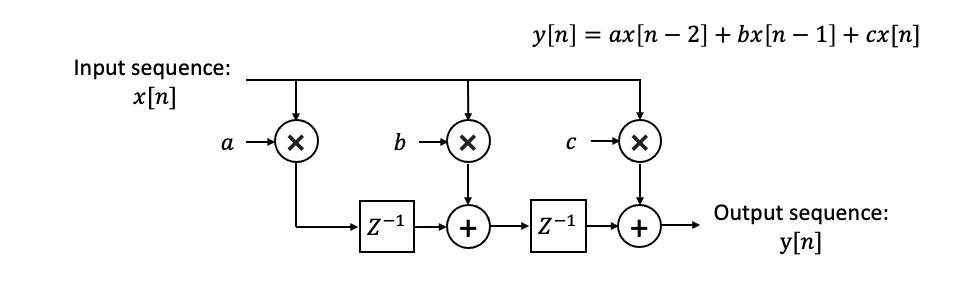
, where the coefficient is \(a = 0.2\), \(b = 0.6\), and \(c = 0.2\). Therefore, \(y[n] = 0.2 \times x[n-2] + 0.6 \times x[n-1] + 0.2 \times x[n]\).
Assume the word lengths of all variables in the system are (6, 0). We can obtain the upper bound error of the output as the previous example:
def example2_filter_design() -> None:
"""Example showing the composition of the filter design"""
in1 = PortWordLength(n=6, p=0, e=0, name="in1")
in2 = PortWordLength(n=6, p=0, e=0, name="in2")
in3 = PortWordLength(n=6, p=0, e=0, name="in3")
const1 = PortWordLength(n=6, p=0, name="const1")
const2 = PortWordLength(n=6, p=0, name="const2")
const3 = PortWordLength(n=6, p=0, name="const3")
mult_out1 = PortWordLength(n=6, p=0, name="mult_out1")
mult_out2 = PortWordLength(n=6, p=0, name="mult_out2")
mult_out3 = PortWordLength(n=6, p=0, name="mult_out3")
add_out1 = PortWordLength(n=6, p=0, name="add_out1")
add_out2 = PortWordLength(n=6, p=0, name="add_out2")
a = 0.2
b = 0.6
c = 0.2
const1.value = float_to_bin(a, const1)
const2.value = float_to_bin(b, const2)
const3.value = float_to_bin(c, const3)
const1.e = a - const1.value_num()
const2.e = b - const2.value_num()
const3.e = c - const3.value_num()
print(f"truncated coefficient: {a} to {const1.value_num()}")
print(f"truncated coefficient: {b} to {const2.value_num()}")
print(f"truncated coefficient: {c} to {const3.value_num()}")
c1 = form_contract_mult_const(in_port=in1, in_port_const=const1, out_port=mult_out1)
c2 = form_contract_mult_const(in_port=in2, in_port_const=const2, out_port=mult_out2)
c3 = form_contract_mult_const(in_port=in3, in_port_const=const3, out_port=mult_out3)
ci1 = form_contract_input(in_port=in1)
ci2 = form_contract_input(in_port=in2)
ci3 = form_contract_input(in_port=in3)
contract1 = PolyhedralIoContract.from_dict(c1)
contract2 = PolyhedralIoContract.from_dict(c2)
contract3 = PolyhedralIoContract.from_dict(c3)
contract_i1 = PolyhedralIoContract.from_dict(ci1)
contract_i2 = PolyhedralIoContract.from_dict(ci2)
contract_i3 = PolyhedralIoContract.from_dict(ci3)
c4 = form_contract_add(in_port1=mult_out1, in_port2=mult_out2, out_port=add_out1)
c5 = form_contract_add(in_port1=add_out1, in_port2=mult_out3, out_port=add_out2)
contract4 = PolyhedralIoContract.from_dict(c4)
contract5 = PolyhedralIoContract.from_dict(c5)
contract_system = contract_i1.compose(contract1)
contract_system = contract_system.compose(contract_i2)
contract_system = contract_system.compose(contract2)
contract_system = contract_system.compose(contract_i3)
contract_system = contract_system.compose(contract3)
contract_system = contract_system.compose(contract4)
contract_system = contract_system.compose(contract5)
print(str(contract_system))
example2_filter_design()
truncated coefficient: 0.2 to 0.1875
truncated coefficient: 0.6 to 0.59375
truncated coefficient: 0.2 to 0.1875
Port: , (n, p) = (12, 0), e = 0, a = 0.999755859375
Port: , (n, p) = (12, 0), e = 0, a = 0.999755859375
Port: , (n, p) = (12, 0), e = 0, a = 0.999755859375
InVars: []
OutVars:[add_out2_a, add_out2_e]
A: [
]
G: [
add_out2_e <= 0.0769
add_out2_a <= 0.9536
]
The result shows that the upper bound error of the output add_out_e is 0.07690.
Note that the upper bound is not tight as we abstract the calculation and consider the worse case truncation error for each operation. The worst case might not happen in all operations simultaneouly, and thus the bound is pessimistic. However, a pessimistic bound still allows us to analyze the design. If the obtained error is smaller than the specification, we can rest assured that the design already satisfies the system specification.
Though it is sufficient for us to efficiently obtain an upper bound and perform optimization to get a better design, we still want to know how tight the bound is. In the following, we try to enumerate all input combinations to find the actual maximum error:
def example_enumerate_error() -> None:
"""Find the actual bound by enumerating the input combinations"""
in1 = PortWordLength(n=6, p=0, e=0, name="in1")
in2 = PortWordLength(n=6, p=0, e=0, name="in2")
in3 = PortWordLength(n=6, p=0, e=0, name="in3")
const1 = PortWordLength(n=6, p=0, name="const1")
const2 = PortWordLength(n=6, p=0, name="const2")
const3 = PortWordLength(n=6, p=0, name="const3")
mult_out1 = PortWordLength(n=6, p=0, name="mult_out1")
mult_out2 = PortWordLength(n=6, p=0, name="mult_out2")
mult_out3 = PortWordLength(n=6, p=0, name="mult_out3")
add_out1 = PortWordLength(n=6, p=0, name="add_out1")
add_out2 = PortWordLength(n=6, p=0, name="add_out2")
a = 0.2
b = 0.6
c = 0.2
const1.value = float_to_bin(a, const1)
const2.value = float_to_bin(b, const2)
const3.value = float_to_bin(c, const3)
diff_max: float = 0
a_max: float = 0
i1_max: float = 0
i2_max: float = 0
i3_max: float = 0
for i1, i2, i3 in itertools.combinations(range(0, 2**6), 3):
i1_float = i1 / 2**6
in1_a = float_to_bin(i1_float, in1)
in1.value = in1_a
i2_float = i2 / 2**6
in2_a = float_to_bin(i2_float, in2)
in2.value = in2_a
i3_float = i3 / 2**6
in3_a = float_to_bin(i3_float, in3)
in3.value = in3_a
port_mult(in1, const1, mult_out1)
port_mult(in2, const2, mult_out2)
port_mult(in3, const3, mult_out3)
port_add(mult_out1, mult_out2, add_out1)
port_add(add_out1, mult_out3, add_out2)
actual_result = add_out2.value_num()
ideal_result = i1_float * a + i2_float * b + i3_float * c
diff = ideal_result - actual_result
if diff > diff_max:
diff_max = diff
i1_max = i1_float
i2_max = i2_float
i3_max = i3_float
if actual_result > a_max:
a_max = actual_result
print(diff_max, i1_max, i2_max, i3_max, a_max)
example_enumerate_error()
0.06874999999999998 0.828125 0.890625 0.90625 0.90625
The actual bound is about \(0.0687\), which is slightly smaller than our derived bound of \(0.0769\). This verifies that our upper bound error is indeed an upper bound for all input combinations.